Integração Aproximada pelo Método do Trapézio

Ontem, um estudante que assistiu minha série sobre Portugol Studio no Youtube entrou em contato comigo. Ele queria saber como implementar o Método dos Trapézios para integrais no Portugol Studio, então resolvi compartilhar toda a teoria e a implementação final aqui. É importante que, para compreender 100% o que vai ser dito aqui, o leitor já tenha estudado Cálculo I. Vamos lá!

Cálculo

Primeiramente, vamos analisar a definição precisa de integral através do método do ponto médio. A integral se propõe, no caso $\mathbb{R}^2$, a calcular a área exata sob o gráfico de uma função (ou o volume no caso $\mathbb{R}^3$) no intervalo $[a,b]$. Para isso, podemos dividir o eixo $x$ em $n$ subintervalos. Para cada subintervalo, escolhemos um $x_i^*$ e definimos a área desse subintervalo como $f(x_i^*)\cdot \Delta x$, em que $\Delta x$ é o tamanho do subintervalo (dado por ${(b-a)/n}$).

A Figura 1 abaixo mostra as diversas somas com $n=4$, $n=8$, $n=16$ e $n= 32$. Observe que, quando $n$ aumenta, a soma das áreas de cada subintervalo se aproxima da área sob o gráfico da função.

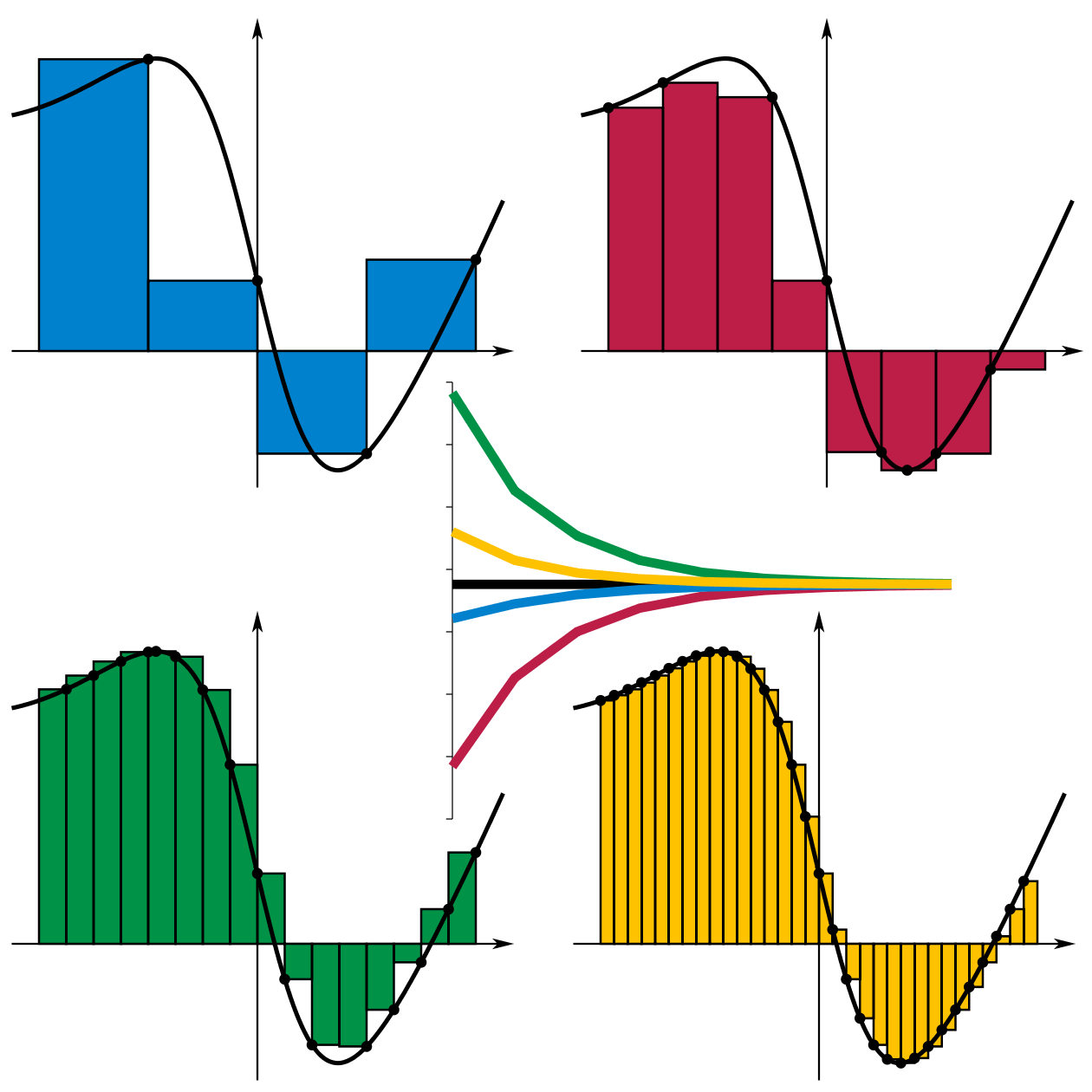
Figura 1: Somas convergindo.

Isso pode ser representado, matematicamente, por: $A \approx \sum\limits_{i=1}^n {f(x_i^*)\cdot \Delta x}$

Sendo assim, se tomamos o limite quando $n \to \infty$, então obtemos uma soma perfeita:

$\int\limits_a^b{f(x)dx} = \lim_{n \to \infty} {\sum\limits_{i=1}^n {f(x_i^*)\cdot \Delta x}}$

Infelizmente, são muitos os casos em que é simplesmente impossível calcular o limite infinito para encontrar uma integral exata. Daí recorremos a métodos de aproximação. Apenas remover o limite e escolher um $n$ arbitrariamente grande é chamado de Método dos Retângulos. Um outro método, com um erro bem menor, é o Método dos Trapézios, ou Integração Trapezoidal.

Nesse método, em vez de somar vários retângulos, cada um aproximando a área entre $x_{i-1}$ e $x_i$, usamos trapézios. Veja na Figura abaixo a comparação entre os dois métodos.

Figura 2(a): Integração por Retângulos.

Figura 2(b): Integração Trapezoidal.

A implementação desse método é parecida com o dos retângulos. Começamos dividindo o intervalo de integração $[a,b]$ em $n$ subintervalos de tal forma que $\Delta x = \frac{b-a}{n}$.

A área do trapézio é dada por: $\frac{(B+b)\cdot h}{2}$ Em que $B$ e $b$ são as bases do trapézio e $h$ é a altura. No nosso caso (considere o $i$-ésimo subintervalo), a “altura” do trapézio é $\Delta x$, ao passo que as bases são $f(x_i)$ e $f(x_{i-1})$.

Observação: note que $x_0 = a$ e $x_n = b$ .

Podemos, então, tomar um $n$ arbitrariamente grande e teremos a integral aproximada:

$\int\limits_a^b {f(x)dx} \, \approx \, \sum\limits_{i=1}^n {\frac{[f(x_i) + f(x_{i-1})]\cdot \Delta x}{2}}$

Como ${\Delta x}/{2}$ é uma constante, pode ser removido da soma.

$\int\limits_a^b {f(x)dx} \, \approx \, \frac{\Delta x}{2}\sum\limits_{i=1}^n {[f(x_i) + f(x_{i-1})]}$

Então temos a equação final para o método dos trapézios. Basta, agora, implementá-lo.

Veja a implementação:

• Portugol Studio
• Python